Quantum theory

Introduction
Our activities cover theoretical and computational problems in quantum information science as well as experimental realizations of quantum devices. Our current theoretical efforts are focused on engineered environments for superconducting qubits, and designing various physical control protocols related to quantum information processing.
The quantum computer is currently one of the most discussed future breakthroughs in science and engineering. Robust quantum bits, or qubits, have been realized using, for example, superconducting circuits, quantum dots, and trapped ions. The state of a qubit is affected by various sources of error such as finite qubit lifetime, measurement imperfections, non-ideal initialization, and imprecise external control. Provided that these errors are below a certain threshold, they can be corrected with quantum error correction codes, which encode the information of a logical qubit into an ensemble of physical qubits. Error correction codes with exceptionally high thresholds, such as surface codes, typically require thousands of physical qubits for each fault-tolerant logical qubit. Although great progress has been made in the recent years to improve qubit control, measurement, and lifetime, simply scaling up with the current state-of-the-art methods would still require a vast amount of physical resources to realize a computationally useful quantum computer.
Tunable environments for quantum circuits
Quantum-circuit refrigeration and heating by photon-assisted tunneling
Fast and accurate initialization of superconducting quantum circuits to a pure quantum state has remained challenging although it is a key requirement in their efficient operation. A solution could be an active refrigerator evacuating entropy on demand. Such device may also be utilized for robust ground-state operation of quantum circuits by reduction of errors related to thermal and non-adiabatic excitations.
We focus on normal-metal–insulator–superconductor tunnel junctions coupled to a superconducting resonator, see figure below. The refrigeration occurs at junction bias voltages where the normal-metal electron needs to receive an additional energy quantum from the coupled quantum electric circuit to overcome the energy gap in the superconductor. The resulting tunability with the bias voltage offers promising technique to quickly evacuate entropy and thus initialize quantum systems on demand.
Starting from the first-principles we theoretically derived [Phys. Rev. B 96, 094524 (2017)] the relaxation and excitation rates induced on a superconducting resonator which is capacitively coupled to NIS junctions. This model accurately describes the physics of the quantum-circuit refrigeration and heating demonstrated in Refs. [arXiv:1612.06822 (2016), Nat. Commun. 8, 15189 (2017)]. Additionally, we are able to capture fine details of the physical circuit, multiphoton states, and multiphoton absorption. In future, we will apply our theory for the full spectrum of of superconducting quantum devices.
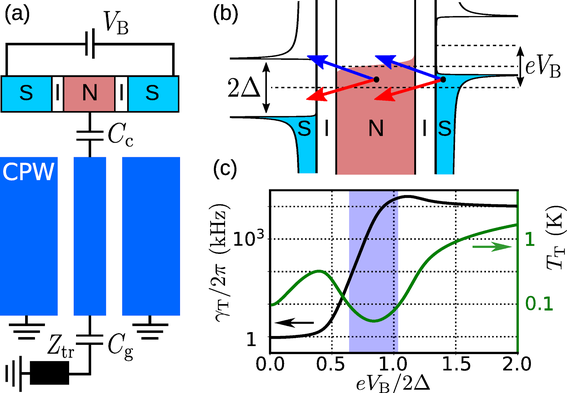
Figure. Schematic diagram of a resonator connected to a normal-metal island and a transmission line from [Phys. Rev. B 96, 094524 (2017)]. The superconductor (S)–insulator (I)–normal-metal (N) tunnel junctions defining the island are voltage biased. (b) Energy diagram of the photon-assisted electron tunneling. The blue arrows depict tunneling events leading to absorption of a photon from the coupled resonator and the red arrows correspond to emission. (c) Coupling strength and temperature of the effective thermal reservoir formed by the photon-assisted tunneling as a function of the two-junction voltage bias. The parameters correspond to typical experimental value. Figure credit: Matti Silveri.
Qubit initialization with tunable coupling to environment
Initialization to a predetermined pure state is a key requirement for quantum computational algorithms and especially for quantum error correction. We have proposed a ground-state initialization circuit where a qubit is coupled to a low-temperature bath through a tunable resonator. We have shown that the qubit lifetime can be decreased by several orders of magnitude by tuning the initially detuned resonator on resonance with the qubit [Sci. Rep. 3, 1987 (2013); J. Low Temp. Phys. 173, 152 (2013)].
Recently, we have developed a protocol for on-demand qubit initialization [npj Quantum Information 3, 27 (2017)]. By using a Markovian master equation, we have shown that the speed of the protocol is determined by the strength of the coupling with the bath, and found a lower bound for the duration of the protocol at a given fidelity. For optimized circuit parameters, we have estimated that the current benchmarks for fidelity and protocol speed can be improved considerably with our protocol.

Figure. Transition rates (above) for the three lowest excited states of the system and the protocol (below) as a function of the control parameter . We have added a second resonator which acts as an additional filter for the qubit and can be used for the qubit-state measurement.
We are currently developing a superconducting circuit realization of our protocol. For further details, see our research page on Tunable environments for superconducting circuits. In the future theoretical work, we will study the protocol when the coupling to the environment is strong and the approximations of the Markovian master equations do not hold. Also, we will use optimal control to improve our protocol.
Numerically exact methods for open quantum systems
Ideally, the quantum devices of the future consist of quantum systems that can be controlled but are otherwise isolated from the rest of the world. In practice, there always exists decoherence caused by a coupling between the system and its surroundings which is typically referred to as the environment. The environment is often modelled with a bosonic bath which consists of harmonic oscillators at thermal equilibrium and is coupled bilinearly to the system. This coupling perturbs the coherent time evolution of the system and, thus, cause errors in the fidelity of the device.
Such errors are conventionally estimated theoretically with Markovian master equations for the reduced density operator of the system. These equations typically rely on a set of approximations, i.e. Born, Markov and secular approximations, which all become inaccurate at low temperatures and when the coupling to the environment is strong. However, the time evolution can also be solved exactly in the path-integral formalism which can be transformed into the form of the stochastic Liouville—von Neumann equation. In addition to accurate description of the decoherence processes, this allows the estimation of errors caused by the above-mentioned approximations. Such estimations will most likely become important in the future information processing devices that operate at the quantum level and require high precision.
We are currently developing a numerical solver for the stochastic Liouville–von Neumann equation. This allows us to study the effects typically neglected or unattainable with master equations, such as the Lamb shift and entanglement with the bath, as a function of the bath coupling strength. The magnitudes of these corrections are especially interesting in the contexts of the single-qubit gate operations, decay rate, and fidelity. We will also study the influence of the bath coupling strength on a two-qubit system, e.g. on the entanglement between two qubits.
Energy-efficient qubit control
Precise single-qubit gates are an essential part of a quantum computer. We have derived [npj Quant. Inf. 3, 17 (2017)] from the quantum-mechanical photon–qubit interactions, for the first time, the greatest lower bound for the error of a single-qubit gate implemented with a pulse of given energy. This result implies that even with a flawless physical implementation, a large-scale quantum processor necessarily faces serious challenges in the heat management. We present a practical scheme how the control pulse can be reused in the quantum processor, leading to orders of magnitude lower heat dissipation.
The above-mentioned derivation also allowed us to solve the quantum state of the controlling mode that minimizes the error of a given single-qubit gate. Specifically, we have shown that the optimal way to perform a rotation on a superconducting qubit is to use so-called squeezed coherent states or squeezed cat states, depending on the desired rotation angle.
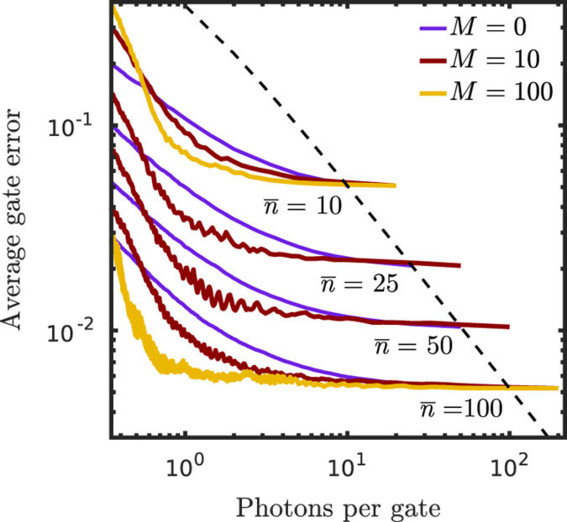
Figure. Average gate error as a function of the average number of photons consumed per gate from [npj Quant. Inf. 3, 17 (2017)]. The dashed line shows the error for disposed coherent pulses (the susual way) and the solid lines show the results of our pulse recycling protocol with different numbers of ancillary qubits. Figure credit: Joni Ikonen.
Precise control of bosonic quantum states
The storage and manipulation of the quantum state of photons is another integral component for the implementation of quantum information processing. In particular, coherent states of photons serve as the reference state or the starting point in various measurement and control schemes, and error correcting codes.
We are investigating a method to maintain the state of a slowly dissipating cavity mode by constantly performing minute corrections that do not require active monitoring. The corrections are produced by resonant interactions with a qubit that is is periodically reset to its ground state by a tunable electromagnetic environment. As a result, the cavity state converges towards a chosen coherent state at a rate that is several orders of magnitude higher than the decay rate of a high-quality cavity. Thus any losses that occur in the cavity are corrected significantly faster than the direct driving of a cavity would allow.
New measurement scheme for superconducting qubits
We are currently working on a new way to measure superconducting qubits with several potential benefits over the usual method of measuring a microwave reflection from a resonator coupled to the qubit.






