Quantum gases

Introduction to BEC
Bose-Einstein condensation (BEC) is a manifestation of macroscopic occupation of a single quantum state. The idea of such phenomenon dates back to 1924-1925, when Albert Einstein extended the statistical arguments presented by Satyendra Nath Bose to systems consisting of a conserved number of bosonic particles. Einstein recognised that at sufficiently low temperatures the quantum statistical distribution of an ideal gas of bosons shows condensation of a macroscopic fraction of the material into the ground state of the system. This phenomenon, subsequently termed Bose-Einstein condensation, is a unique, purely quantum-mechanical phase transition in the sense that it occurs in principle even in noninteracting bosonic systems.
A breakthrough in realizing the original idea of BEC occurred in 1995, when research groups at University of Colorado, MIT, and Rice University observed convincing evidence of BEC in dilute alkali atom clouds. These pioneering experiments, from which the Nobel prize was awarded in 2001, launched an avalanche of theoretical and experimental research on the physics of weakly interacting atomic condensates. Due to weak interactions, these systems are rare examples of interacting quantum gases amenable to detailed quantitative analysis, and thus provide unique possibilities for testing the fundamental principles and theories of many-particle quantum physics and even simulating physical phenomena and devices.
Overview of our BEC research
One of the most fundamental branches of research in QCD group is the studies on coherent matter fields, that is Bose-Einstein condensates (BECs) of dilute atomic gases. In BEC research community, we are best-known from the development of methods to create and creation of monopoles, quantum knots, skyrmions, and multi-quantum vortices into the condensate by control of the external magnetic fields.
Some time ago, we introduced a robust method to create Dirac monopoles into the condensate utilizing adiabatic control of the the external magnetic fields [Phys. Rev. Lett. 103, 030401 (2009) PRESS RELEASE]. Consequently, we reported the observations of Dirac monopoles in the synthetic magnetic field [Nature 505, 657 (2014) PRESS RELEASE] and isolated monopoles, i.e. quantum-mechanical point defects, in the quantum field [Science 348, 5644 (2015)]. All the experimental results have been achieved in collaboration with Prof. David S. Hall’s group at Amherst College, USA. We have also investigated the creation of non-Abelian monopoles in these systems, but thus far only theoretically [Phys. Rev. Lett. 102, 080403 (2009)].
Our studies of topology in spin-1 BECs also involve defects belonging to the third homotopy group, namely skyrmion and knot structures. In our experimental collaboration, we have observed quantum knots [Nat. Phys. 12, 478 (2016)] and Shankar skyrmions [Sci. Adv. 3, eaao3820 (2018)]. We have furthermore proposed methods to create quantum knots using the so-called counterdiabatic magnetic field [Phys. Rev. A 96, 063609 (2017)] and skyrmionic structures in spin-2 BECs using quadrupole magnetic field [New J. Phys. 20, 055011 (2018)].
Furthermore, we have introduced cyclic vortex creation procedure, which resulted in a so-called vortex pump, that is, a method to cyclically increase the vorticity of the system rendering it possible to create giant vortices [Phys. Rev. Lett. 99, 250406 (2007); J. Low Temp. Phys. 161, pp. 561 (2010)]. Also the dynamics of these giant vortices is of our interest [Phys. Rev. Lett. 97, 110406 (2006); Phys. Rev. Lett. 99, 200403 (2007); Phys. Rev. A 81, 033627 (2010)]. We have also studied so-called coreless vortices in spinor BECs [Phys. Rev. A 79, 023618 (2009)].
Our research interests also span rotating multi-component BECs [Phys. Rev. A 85, 043613 (2012)] as well as elementary excitations, both dipolar and spin-orbit coupled condensates [Phys. Rev. A 82, 053616 (2010);Phys. Rev. A 84, 043638 (2011); Phys. Rev. A, 86, 051607(R) (2012)] and vortex dipoles [Phys. Rev. A 83, 011603(R) (2011)].

Artistic illustration of a synthetic magnetic monopole on our work [Nature 505, 657 (2014)] where we experimentally created a Dirac monopole in the synthetic magnetic field of a spin-1 BEC. Figure credit: Heikka Valja.
Monopoles in BECs
The question of the existence of a magnetic monopole dates thousands of years back in history when the ancient Greek philosophers found that when breaking a magnetic rock, a new south and north pole is created to the break points. In 1931, Paul Dirac made his initial studies on magnetic monopoles interacting with quantum fields. He combined arguments from quantum mechanics and classical electrodynamics and identified electromagnetic potentials and solutions of the Schrödinger equation consistent with the existence of magnetic monopoles. Because of far-reaching implications to classical, quantum, and particle physics, the experimental observation of monopoles in quantum fields is of great interest. Due to failure of all experiments trying to find monopoles in natural magnetic fields, there have been many suggestions to experimentally observe monopoles in analogous quantum fields.
In Ref. [Phys. Rev. Lett. 102, 080403 (2009)], we theoretically studied so-called non-Abelian monopoles induced by an artificial magnetic field due to a laser driving transitions between the different hyperfine spin states of the atoms. Although the non-Abelian monopole is conceptually interesting and desirable to realize in the experiments, it has the drawback that the monopole forms in the pseudo spin and not the true hyperfine spin of the atoms. Furthermore, the non-Abelian nature may be challenging to measure in the experiments. Thus we began to study how to create Abelian Dirac monopoles in the condensates by using an adiabatic phase imprinting method. It turned out that by using the combination of a homogeneous bias field and a three-dimensional quadrupole field, it is possible to create a Dirac monopole [Phys. Rev. Lett. 103, 030401 (2009)] into the vorticity field of the condensate. The figure below shows how the creation of the Dirac monopole by adiabatically moving the zero-point of the magnetic field into the optically trapped BEC that is initially in its defect-free ground state.
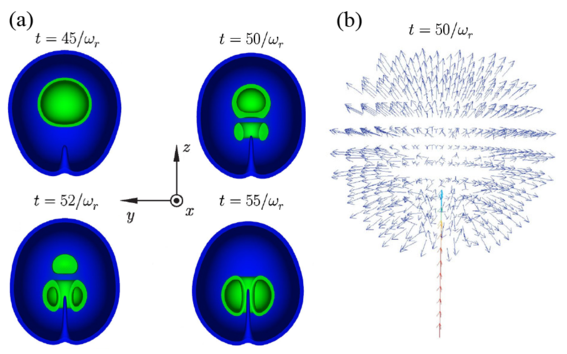
Figure. (a) Particle density isosurfaces (cut for clarity) and (b) vorticity of the condensate during the creation process of a Dirac monopole. In panel (b), the monopole is manifested in the hedgehog structure of the vorticity and the Dirac string is clearly visible as the red line terminating at the monopole. In panel (a), the Dirac string shows as a depletion of the particle density along it. Figure credit: Ville Pietilä.
Four years later, the long-awaited first experimental realization and observation of the Dirac monopole in a quantum field was achieved using this method. This achievement was a fruit of our collaboration with the group of Prof. David S. Hall (Amherst College, USA) and our results were published in Nature [Nature 505, 657 (2014)]. The figure below shows the comparison between the experimental and the simulated data when the Dirac monopole is near the center of the atomic cloud.
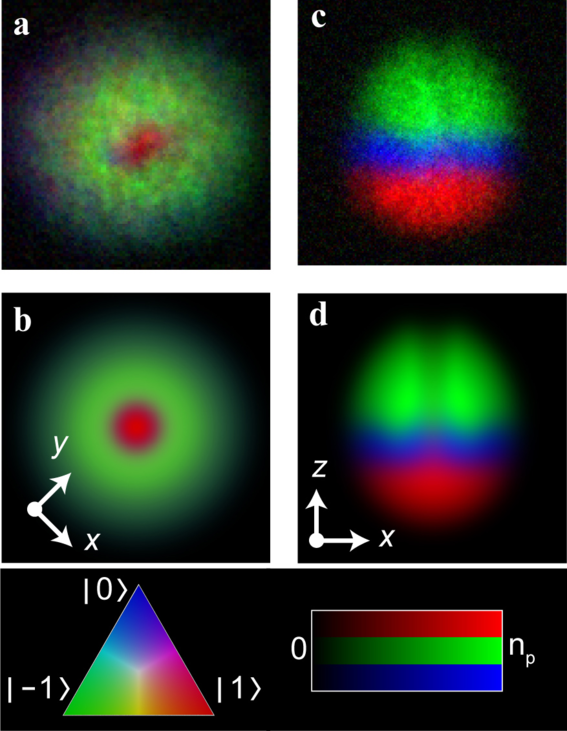
Figure. Experimental (a),(c) and simulated (b),(d) particle densities in the spinor components when the monopole is near the center of the condensate. The Dirac string is visible as depleted density in spinor components l-1> and l0>. Figure credit: Michael Ray.
Although this is a great achievement and first realization of Dirac’s over 80-year-old theory, the condensate spin-1 order parameter does not have a monopole singularity. The monopole is in the so-called synthetic magnetic field, i.e., the scalar part of the condesate order parameter moves as if it was a charged particle in the static magnetic field of a magnetic monopole. However, the natural magnetic monopole is predicted to be a topological monopole defect also in the quantum field of grand unified theories. Fortunately, the so-called polar phase of the spin-1 BEC supports topological point defects, and once we used the same method that was used to create Dirac monpoles in the ferromagnetic phase to the polar phase, we were able to create the first topological point defects in the realm of quantum mechanics [Science 348, 5644 (2015)]. These are real monopoles, although only analogues of natural magnetic monopoles.

Figure. Artistic illustration of an isolated monopole on our work [Science 348, 5644 (2015)] where we experimentally created a topological point defect into a spin-1 BEC. Figure credit: Heikka Valja.
The experimental discoveries of monopoles opened up many new research avenues. For example, the dynamics and the decay of monopoles are of particular interest as the monopole is not created in the ground state [Phys. Rev. A 84, 063627 (2011)]. We have theoretically studied the evolution of the isolated monopole in the presence and absence of a quadrupole magnetic field [Phys. Rev. A 93, 033638 (2016), Phys. Rev. A 94, 053616 (2016)]. Soon after we confirmed the theoretical prediction of an isolated monopole to decay into a Dirac monopole during its temporal evolution [Phys. Rev. X 7, 021023 (2017)]. Interestingly, we observed spontaneously appearing nodal lines related to the Dirac monopole. In the first Dirac monopole experiments, these nodal lines are imprinted onto the path traced by the zero point of the quadrupole field, but here they spontaneously appear in a configuration which tends to minimize energy. The nodal lines are a direct consequence of Dirac’s old theory telling that if (synthetic) magnetic monopoles exists, there has to be one or many ending lines of vanishing particle density on the wave function of a (synthetically) charged particle interacting with the monopole.

Figure. Dirac monopoles which have been created by waiting for an isolated monopole to decay. (from left to right) Experimental particle column densities in the xy-plane for each spin component, color composite density in the xz-plane, and simulated 3D particle density isosurfaces. Each row represents a different vertical location of the monopole as controlled by the creation process. Figure credit: Tuomas Ollikainen.
Knots in BECs
Knots are topologically stable objects in field theories and they have been put forward to explain various persistent phenomena in systems ranging from atoms and molecules to cosmic textures in the universe. Skyrmions were initially predicted in the 1960s in the context of field theories in particle physics. Recently they have gained a wide range of interest in the area of condensed matter physics.
Both knots and skyrmions correspond to the topologically nontrivial elements of the third homotopy group but the difference is that knots assume a certain value of the field along loops whereas in skyrmions the values are achieved at isolated points. To our knowledge, no other experimental images of elements of the third homotopy group have been reported.
From our studies of the isolated monopole, we know that the direction of the three-dimensional quadrupole field has a topological point defect in it, i.e., the field assumes all possible directions twice on a surface that encloses the zero point. Furthermore, the field strength increases linearly with distance from the zero point. Thus if we start with a uniform field in the condensate and suddenly change the field into a configuration where the zero point is inside the condensate, the external field starts to induce rotations about all possible directions. And the rotation angle smoothly increases from zero at the center to a maximum value at the boundary of the condensate. Thus if we choose the waiting time such that we obtain a full 2π rotation at the boundary, we end up introducing every possible rotation to the condensate spinor twice while leaving the spinor unchanged at the boundary. Why twice? Because if you add an angle π to a rotation, you obtain the same rotation by the axis is reversed.
The above described procedure is identical to that used to create Dirac and isolated monopoles except we make the field ramp suddenly rather than adiabatically. Consequently, we created the first quantum knots in [Nat. Phys. 12, 478 (2016)] by starting from the polar order parameter. The magnetic order of the polar order parameter is described by just a real 3D vector, and hence the rotation angle about the direction itself makes no difference. This is why we end up with a quantum knot structure shown below. Interestingly, the functional form of the order parameter matches the celebrated Hopf fibration. This is why the created object may also be called a Hopfion. In [Phys. Rev. A 96, 063609 (2017)], we found theoretically a way to create the quantum knots by quickly sweeping the zero point through the condensate rather than by waiting. This method was shown to be compatible in creating nested structures of many knots.

Figure. Visualization of the quantum knot created in [Nat. Phys. 12, 478 (2016)]. Each color represents certain directions of the magnetic order in the spin-1 condensate. Each direction forms a loop and all loops are linked exactly once, thus forming a knotted structure. Figure credit: David Hall.
Skyrmions in BECs
Very recently, we use the same method that was employed to create quantum knots to create three-dimensional skyrmions [Sci. Adv. 3, eaao3820 (2018)]. This time we begin with the ferromagnetic order parameter where the spin is pointing up everywhere. After suddenly bringing in the quadrupole zero and waiting for a full 2π rotation to occur at the boundary of the condensate, the spin vector arranges itself into a configuration of the quantum knot given above. However, the topological defect in the condensate is not a quantum knot but a skyrmion since in addition to the direction of the spin, the order parameter has a quantum phase that corresponds to a rotation angle about the direction of the spin. This quantum phase is related to the particle current density in the condensate, and hence is physically observable. Since the phase winds by an angle of 2π along each loop of constant spin direction, the condensate assumes every physically distinct magnetic orientation exactly twice inside the skyrmion.
Curiously, we computed the synthetic magnetic field that is induced by the skyrmion and noticed that is exactly matches the field proposed in [Nature 383, 32 (1996)] for a ball lighting. The field lines of the synthetic magnetic field are knotted and hence provide another realization of the Hopf fibration in our system.

Figure. Artistic impression of a quantum ball lighting related to our work in [Sci. Adv. 3, eaao3820 (2018)]. Figure credit: Heikka Valja.
Vortices in BECs
In a contrast to superfluid 4He, BEC of alkali-metal atoms has the hyperfine spin degree of freedom which can be utilized to create vortices. We have been studying a method which is referred to as the topological phase imprinting. Note that the above-discussed method to create monopoles and knot is an extension of topological phase imprinting to three dimensions.
We have shown that with suitable choice of external magnetic fields, it is possible to create two- and four-quantum vortices into the condensate [Phys. Rev. A 66, 013617 (2002); J. Phys.: Condens. Matter 14, 13481 (2002)]. When the fields are adjusted such that the condensate dynamics is adiabatic the result can be interpreted as the accumulation of geometric phase, the Berry’s phase, for individual spins of the condensate atoms. This method has been experimentally verified by Wolfgang Ketterle’s group at MIT [Phys. Rev. Lett. 89, 190403 (2002)] together with observations on the splitting of the vortex [Phys. Rev. Lett. 93, 160406 (2004)] which we have also managed to simulate successfully [Phys. Rev. A 68, 023611 (2003); Phys. Rev. Lett. 97, 110406 (2006)]. Since our method relies only on the topology of the external magnetic fields, it is particularly robust for the possible noise in the external fields.
We extended this idea of topological vortex formation into a so-called vortex pump, in which the vorticity of the condensate is increasing by a constant amount during each pumping cycle [Phys. Rev. Lett. 99, 250406 (2007)]. A modified pumping cycle utilizing time-averaged orbiting potential trap was recently investigated and the results were published in Ref. [Phys. Rev. A 87, 033623 (2013)]. See also closely related Refs. [J. Low Temp. Phys. 161, 561 (2010); Phys. Rev. A 81, 023603 (2010)]. For more information on the topological vortex formation see our article [Topological vortex creation in spinor Bose-Einstein condensates, in a book Electromagnetic, magnetostatic, and exchange-interaction vortices in confined magnetic structures, E. O. Kamenetskii (Eds.), (Research signpost, Kerala), ISBN 978-81-7895-373-1, 2008]
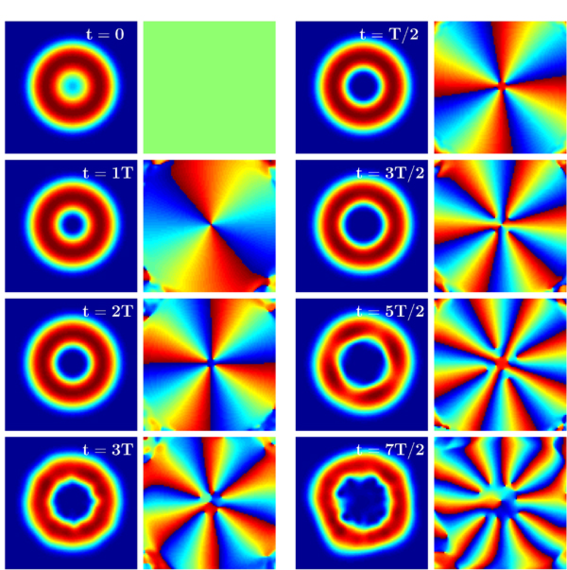
Figure. Pumping vortices in BECs. Particle density (left columns) and complex Phase (right columns) of the condensate.
One of our research interests is the structure and stability of multiply quantized vortices in dilute atomic Bose-Einstein condensates. Doubly and quadruply quantized vortices can be created with the topological phase engineering technique which is also utilized in the vortex pump. Multiply quantized vortices are in general energetically unstable, and they tend to split into singly quantized vortices. The vortices usually intertwine strongly as they split, as shown in the isosurface plot of the condensate density below. Also, dissipation is negligible in the zero temperature limit, and the excess energy is pushed into excitation of surface modes during the splitting process.
We have studied the stability properties of multi-quantum vortices in different trap geometries by solving the Bogoliubov excitation spectra in Ref. [Phys. Rev. A 74, 063619 (2006)]. We have also calculated the splitting times of doubly quantized vortices as a function of particle number in elongated condensates in Ref. [Phys. Rev. Lett. 97, 110406 (2006)] and investigated the dynamics of the splitting of quadruply quantized vortices in Ref. [Phys. Rev. Lett. 99, 200403 (2007)]. More recently, we studied how giant vortices with very many circulation quanta split in pancake-shaped condensates and observed that they divide the condensate into a few vortex free regions separated by vortex sheets [Phys. Rev. A 81, 023603 (2010)]. We are currently in the process of studying the splitting of giant vortices in three-dimensional traps such as a spherical, the results of which are expected to be published in 2018.

Figure. Splitting of a doubly quantized vortex. Cropped particle density isosurface.
Phase transitions
We have investigated various phase transitions in the context of spinor BECs. Low-dimensional systems cannot support true long-range order, but the superfluid phase transition is still possible via the Berezinskii-Kosterlitz-Thouless (BKT) mechanism. In the past, we have studied the BKT transition in antiferromagnetic spinor BECs [Phys. Rev. A 81, 033616 (2010)]. In this case, the BKT transition is mediated by half-quantum vortices (HQVs) and we analysed the thermal activation of HQVs in the experimentally relevant trapped quasi-2D systems. We found that the crossover temperature is shifted upwards if skyrmions are allowed, and above the defect binding temperatures we observe transitions corresponding to the onset of a coherent condensate and a quasi-condensate. We have also investigated the instabilities induced by the long-range magnetic dipole-dipole interaction using renormalization group methods [Phys. Rev. A 84, 013605 (2011)]. In the zero-temperature limit where quantum fluctuations prevail, we found the phase diagram to be unaffected by the dipole-dipole interaction. When the thermal fluctuations dominate, polar and ferromagnetic condensates with dipole-dipole interaction become unstable. On the other hand, a so-called spin-singlet condensate remains stable even in the presence of dipole-dipole interactions.
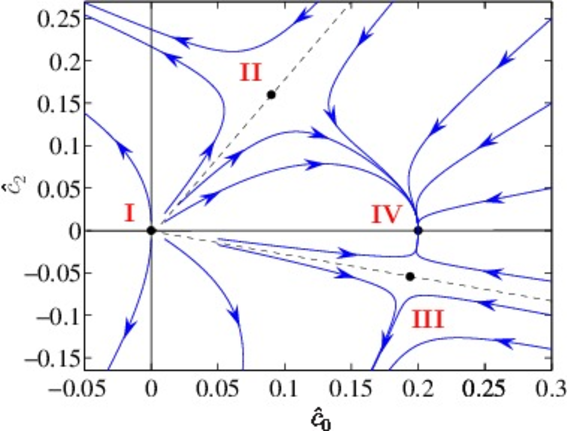
Figure. Renormalization group flow for a three dimensional spin-1 Bose gas at fixed temperature.






