Uncertainty Analysis of Correlated Color Temperature (2014-2017)

Introduction

Metrology Research Institute has made various studies in the area of unknown correlations in spectral irradiance data in project EMRP ATMOZ - Traceability for Atmospheric Total Column Ozone (2014-2017) including an interlaboratory comparison of CCT using old comparison data of spectral irradiance, and developing a Monte Carlo (MC) method for estimating effects of unknown spectral correlations on CCT.

Uncertainty modelling accounting for unknown correlations

Uncertainty is an estimate of possible errors that the data may have. Correlations related with uncertainties predict possible spectrally changing deviations that there might be hidden in the measurement errors, as depicted in the figure. Correlation remains often unknown which is a serious limitation because with spectrally derived quantities, the uncertainties of the calculated results depend heavily on the type of correlation. Noise often averages out, but spectral structures may cause large errors.

In reference [1] we proposed a new method for estimating uncertainties of CCT in cases where spectral correlations are unknown. The method goes through all possible scenarios of deviations using MC analysis. Varying spectral deviation functions are produced by combining spectral base functions, and the distorted spectra are used to calculate the colorimetric quantities. Standard deviations of the colorimetric quantities at different scenarios give uncertainties assuming no correlations, uncertainties assuming full correlation, and uncertainties for an unfavorable case of unknown correlations, which turn out to be a significant source of uncertainty.

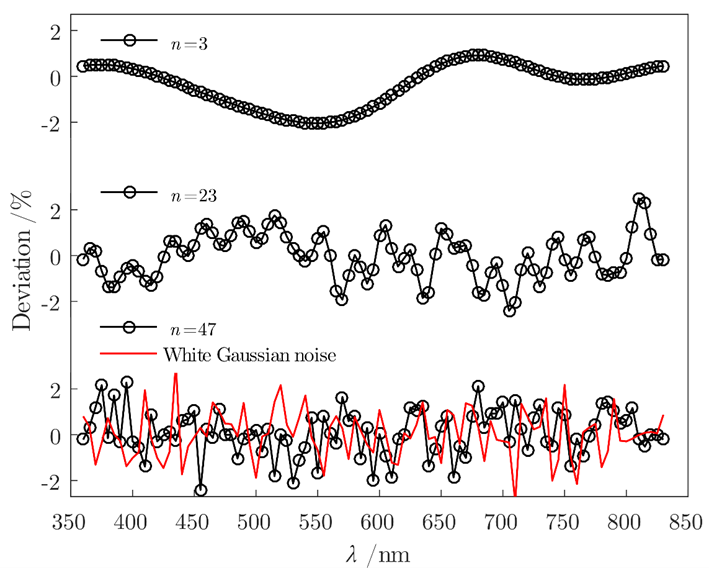
With 1% standard uncertainty in spectral irradiance, the expanded uncertainty of the correlated color temperature of a source corresponding to the CIE Standard Illuminant A may reach as high as 37.2 K in unfavorable conditions. Calculations assuming full correlation give zero uncertainty, and calculations assuming no correlations yield the expanded uncertainties of 5.6 K and 12.1 K, with wavelength steps of 1 nm and 5 nm used in spectral integrations, respectively. We re-estimated the uncertainties for the colorimetric properties of our 1 kW photometric standard lamps using the new method. The revised uncertainty of color temperature is a factor of 2.5 higher than the uncertainty assuming no correlations.

Intercomparison of Correlated Color Temperature

To demonstrate the effects of correlations in practice, we analyzed the results of spectral irradiance key comparison CCPR-K1.a for CCT [2]. For four participants out of 13, the uncertainties of CCT, calculated using traditional methods, not accounting for correlations, would be too small, as shown in the table.

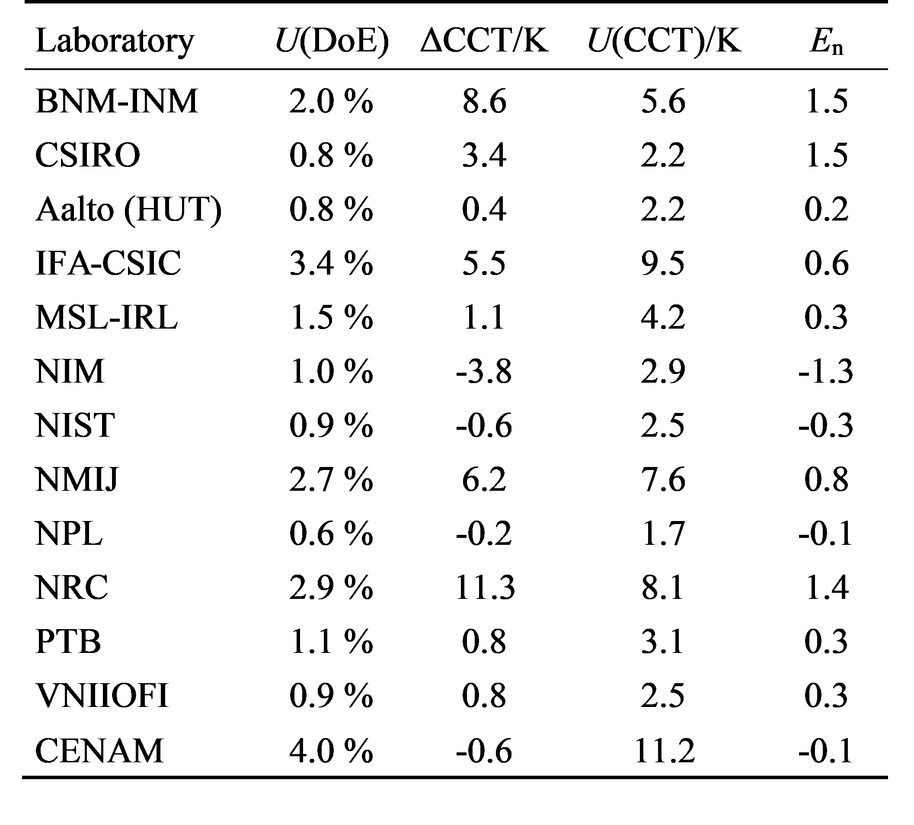
The intercomparison gave useful information about typical correlations in the high-accuracy spectral irradiance calibrations of National Standards Laboratories. On the average, noise only accounts for 20% of uncertainty. 40% of the uncertainty can be characterized as offset, and 40% as severely correlated structural deviation. After using such a lamp for calibration, it can well be assumed that these correlation types are equally present in the further measurements, because noise increases in calibrations. Using this assumption gives safer uncertainty limits than assuming that the traditional assumption that all uncertainty comes from noise.

Contact persons: Petri Kärhä and Anna Vaskuri

References

[1] P. Kärhä, A. Vaskuri, H. Mäntynen, N. Mikkonen, and E. Ikonen, “Method for estimating effects of unknown correlations in spectral irradiance data on uncertainties of spectrally integrated colorimetric quantities,” Metrologia 54, 524 – 534 (2017).

[2] P. Kärhä, A. Vaskuri, T. Pulli, and E. Ikonen, “Key comparison CCPR-K1.a as an interlaboratory comparison of correlated color temperature,” Journal of Physics: Conference Series 972, 012012 (2018).